五分钟经济学|去同存异：“标尺竞争”的逻辑-来谈经济-财新网

提要

“标尺竞争”是一种“利弊互见”的激励机制，其本质是“去同存异”。最著名的例子是中国地方政府所面临的“GDP锦标赛”。

上次分析的效率工资机制，牵涉到最简单的委托代理关系，其中只有一个委托人，一个代理人。但很多情况下，委托代理关系要更加复杂一些。比如，一个委托人可能面临多个代理人，或者一个代理人可能面临多个委托人（这被称为共同代理人问题）。

今天讨论一个委托人，多个代理人的情形，说明委托人是如何利用标尺竞争（yardstick competition）的方法，来一并解决多个代理人的激励问题的。

根据上一期内容可知，一旦委托人需要“激励”代理人努力工作，必然是因为他无法观察到代理人是否在努力工作，而且代理人的业绩与他的努力程度至多存在一种随机对应关系。

的确，如果委托人能把直接观察到代理人的行为，他就可以直接“命令”代理人努力工作；进一步，如果代理人的业绩与努力程度之间存在一对一的确定关系，委托人能观察到代理人业绩，也就相当于能观察到代理人的行为，进而也就可知直接“命令”代理人努力工作。这些情况下，委托人在制定合同时，只需要满足代理人的参与约束就够了，而无需去“激励”他们。

由此，我们做个最简单的假设，有一个委托人，两个代理人，而两个代理人的业绩分别为：

q1=e1+ε1，

q2=e2+ε2，

即代理人1的业绩q1，不光取决于他自己的努力水平e1，还取决于某个随机冲击ε1；尽管委托人能观察到q1，但却无法直接观察到e1和ε1到底取什么值。对代理人2，情况是完全类似的。

很显然，如果两个代理人所遭受的随机冲击ε1和ε2完全不相关，那么，委托人要同时激励两个代理人努力工作的问题，与委托人分别激励两个代理人努力工作的问题，将是完全一样的，也就是上一次所分析的效率工资问题。

但是，如果两个代理人所遭受的随机冲击ε1和ε2具有相关性，情况就会有所不同。最极端的情况是，两个代理人面临着完全相同的随机冲击ε0，即两个代理人的业绩分别为：

q1=e1+ε0，

q2=e2+ε0。

这时候，委托人当然还是可以分别对两个代理人进行激励，但却多了另外一种选择，即“标尺竞争”。“标尺竞争”的道理实际上很简单，虽然委托人观察不到两个代理人的努力程度和随机冲击，但他却知道两个代理人遭受的是完全相同的外生冲击。

由此，如果将两个代理人的业绩相减，这个共同冲击就消失了，而他们的业绩之差也就反映了他们努力程度之差。具体地，代理人1与代理人2之间的业绩之差为：

Δq=q1-q2=e1-e2。

如果Δq>0，即代理人1的“相对业绩”更好，则意味着e1>e2，即代理人1比代理人2更加努力；反过来，如果Δq<0，即代理人1的“相对业绩”更差，则意味着e1<e2，即代理人2比代理人1更加努力。

正因如此，此时委托人可以利用“标尺竞争”来激励两个代理人努力工作：对“相对业绩”更好的代理人进行奖励，力度为B；对“相对业绩”更差的代理人进行惩罚，力度为L；而若两者业绩相同，则既不奖励，也不惩罚。

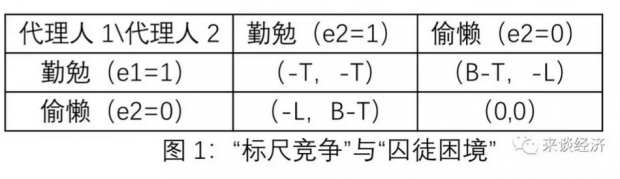
下面，我们参考表1来分析标尺竞争能否奏效。为了尽可能简化分析，我们假设每个代理人只有两种选择，“勤勉”（e=1），或“偷懒”（e=0）；“偷懒”时，努力成本为0，而“勤勉”时，努力成本为T。

进一步假设，奖励和处罚的力度都足够大，即B>T，L>T。“足够大”的含义是，如果“勤勉”能够获得奖励，或者能够避免处罚，代理人都是愿意支付努力成本的。

图1中，第一列代表了代理人1的努力情况，而第一行则代表了代理人2的努力情况。这样，给定每个代理人有两种努力选择，总共就有四种可能的组合；而对应于每个组合，括号里面有两个数字，第一个数字代表了该种组合下代理人1的收益，第二数字代表了该种组合下代理人2的收益。具体地：

（1）如果两个代理人都选择“勤勉”，他们的“相对业绩”相同，Δq=0，故由“标尺竞争”规则，两个人都没有奖惩，但每个人需要支付努力成本T，因而每个人的净收益为-T，而相应的收益组合为（-T，-T）。

（2）如果代理人1选择“勤勉”而代理人2选择“偷懒”，则Δq=1，即代理人1的“相对业绩”更好，故由“标尺竞争”规则，代理人1拿到奖励B，扣除努力成本T，其净收益为B-T；而代理人2受到处罚L，而考虑到他没有努力成本，故其净收益就为-L。所以，此时两个代理人的收益组合为（B-T，-L）。

（3）如果代理人1选择“偷懒”而代理人2选择“勤勉”，则情况与（2）恰好相反，最终两个代理人的收益组合为（-L，B-T）。

（4）如果两个代理人都选择“偷懒”，他们的“相对业绩”也相同，因为都没有努力成本，故这时候他们的收益组合为（0,0）。

下面，我们具体分析两个代理人会如何选择。实际上，我们寻求的是所谓的“纳什均衡”（Nash equilibrium）。在这个例子中，由分析过程，纳什均衡的含义是可以直观理解的。

首先看代理人1会如何选择。

不妨先假设代理人2选择“勤勉”。这时候，如果代理人1也选择“勤勉”，其净收益将为-T；如果他选择“偷懒”，他的净收益为-L。因为L>T，两厢比较下来，他会选择“勤勉”。

不妨再假设代理人2选择“偷懒”。这时候，如果代理人1选择“勤勉”，其净收益为B-T；而如果他也选择“偷懒”，他的净收益为0。因为B>T，两相比较下来，他会选择“勤勉”。

由此可见，不管代理人2选择“勤勉”还是“偷懒”，代理人1的最优选择都是“勤勉”！

然后，基于完全类似的道理，不管代理人1选择“勤勉”还是“偷懒”，代理人2的最优选择也都是“勤勉”。

综合上述分析可知，这个博弈唯一的“纳什均衡”是两个代理人都会选择“勤勉”，相应的收益组合是（-T，-T）。

而“纳什均衡”的含义是：给定代理人1选择均衡策略“勤勉”，代理人2的最优策略也是“勤勉”；反过来也一样，给定代理人2选择均衡策略“勤勉”，代理人1的最优策略也是“勤勉”。也就是说，给定另一方选择了均衡策略，没有人愿意“单方面”偏离他自己的均衡策略。

不难发现，面临委托人所设定的“标尺竞争”机制，两个代理人陷入了所谓的“囚徒困境”（prisoners’ dilemma）：均衡结果下，两个代理人都选择“勤勉”，结果每个人最终所得净收益都为-T；与之相比，如果两个代理人都选择“偷懒”，他们也具有相同的相对绩效，既没有奖励，也没有惩罚，但却无需支付努力成本，因而所得净收益更高，都为0。

站在两个代理人的角度，这是一种“个人理性”最终导致了“集体非理性”的典型例子；虽然他们两个人都很清楚，如果他们相互“合谋”，一起选择“偷懒”，每个人都能获得更好的收益，但对每个人代理人而言，如果另外一个代理人真的选择了“偷懒”，他的最优选择将是“勤勉”，自己获得奖励，而另一方受到处罚。

但站在委托人的角度，正是这个“囚徒困境”机制保证了“标尺竞争”的稳定性和有效性。

稳定性的含义是，尽管两个代理人“合谋”有利可图，但由于各自“心怀鬼胎”，合谋却无法达成，或者即便达成了，也会随时瓦解。这与各种“卡特尔”难以维持是一样的道理。

有效性的含义是，虽然委托人观察不到代理人的努力程度，但凭借标尺竞争的方法，不用花费额外的激励成本，就可以让两个代理人“勤勉”工作。

但是，任何结论的成立都依赖于其先决条件。标尺竞争自然也是如此。对照前面的分析过程，列举如下几点：

第一，两个代理人面临共同冲击。

因为只有是共同冲击，相对业绩才能真正代表他们的努力差异。现实生活中，两个代理人不可能面临完全相同的随机冲击，而更加一般的情况是：

q1=e1+ε1+ε0，

q2=e2+ε2+ε0，

即每个代理人的业绩同时取决于三个方面的因素：其本身的努力水平（e1或e2）,其独特的随机冲击（ε1或ε2），以及共同的随机冲击（ε0）。

如此一来，两个代理人的业绩差就变为Δq=q1-q2=e1-e2+ε1-ε2，这固然消除了“共同冲击”的影响，但却无法消除“个体冲击”的影响。

所以，委托人看到Δq>0，即代理人1具有更好的相对业绩，他将无法确知，这到底是因为代理人1更加努力呢，还仅仅是因为他运气更好，即面临着更加有利的随机冲击。

这时候，委托人针对相对绩效Δq对两个代理人进行奖惩，就不可能做到完全精准的“赏罚分明”，因为一个“勤勉”的代理人可能会因运气太差而受罚，而另一个“偷懒”的代理人则有可能因为运气很好而受到奖励。

第二，两个代理人的业绩指标是可比的。

俗话说，“文无第一，武无第二”。判断两个人谁的文章写得好，这不但取决于文章本身，还取决于读者的偏好，难下定论；但两个人比武，谁把谁打趴下了，非常容易判断。类似的道理，即便两个代理人遭遇共同冲击（比如面临相同的市场环境），但如果他们的业务风马牛不相及，把他们拉在一起比较就没有什么意义。

第三，两个代理人取得好业绩的难度不能有太大的差异。

不妨设想，如果代理人1只要稍稍努力就可以取得好业绩，而代理人2即便花了九牛二虎之力，也只能获得差强人意的业绩，那么，将两个人放在一起进行“标尺竞争”，既不公平，也不有效。

比如说，两个代理人的业绩分别是：

q1=100*e1+ε0，

q2=e2+ε0，

则他们的相对业绩为Δq=q1-q2=100*e1-e2。这时候，如果委托人完全就按照相对业绩来进行奖惩，那么，代理人1只需要花费稍微高于0.01的努力水平，就可以“击败”代理人2，这是非常不公平的竞赛。

进一步，预期到这个结果，代理人2就完全没有努力工作的积极性了，而代理人1也绝不会花高于0.01的努力水平，这显然又是非常没有效率的。

标尺竞争在现实生活中具有极其广泛的应用。比如，要通过考试在一个班级中选拔学习最好的学生，人们最看重的，可能并非这些学生的绝对成绩，而是他们的相对排名。

因为绝对考试成绩，既取决于学生的水平高低，也取决于试卷难度的大小。但是，给定所有学生使用的是同一套试题，那么，他们的相对排名就在很大程度上“剔除”了试卷难度的影响。

下面需要特别强调的一个例子，即中国地方政府之间的“GDP”锦标赛（tournament）。因为这同时展示了标尺竞争带来的巨大好处和坏处。

改革开放以来，中国经济取得了四十年的高速增长，从濒临崩溃迅速成长为世界第二大经济体，堪称“中国奇迹”；但毋庸讳言，高速增长也带来了一系列严峻挑战，比如，环境恶化、重复建设、产能过剩等等。

对于中国经济高速增长的原因及其得失，学界已有很多解释，但普遍认为，这些都与中国特色的央地分权与干部考核机制密切有关。

中国是一个大国，人口众多，地域辽阔，单靠一个中央政府是没有办法进行有效治理的，必须进行央地分权，中央政府是委托人，而各地方政府则是代理人。

给定“以经济建设为中心”，中央政府面临的巨大难题是如何激励地方政府努力工作。诚如毛泽东在《论十大关系》中所而言，中央和地方两个积极性，要比仅仅有中央一个积极性更好。

按照周黎安等人的研究，过去几十年，中央政府凭借强有力的干部任免制度，对各地方政府提供了俗称为“GDP锦标赛”的“标尺竞争”合同：GDP表现相对较好的地方，其地方官员更有可能获得政治上的升迁。

面对这样一个相对绩效考核机制，各地方政府的官员就具有提高自己GDP相对绩效的强烈动机。而要改善自己的相对绩效，本质上两种基本的策略：

第一，“真抓实干”。给定其他地方的GDP，尽可能提高本地方的GDP。

这主要体现为，地方政府官员不懈余力地“招商引资”，以及为了“招商引资”，而大力改善本地基础设施等营商环境。按照张五常在《中国的经济制度》中的解释，中国过去的高速增长，动力主要来源于此。

第二，“以邻为壑”。给定本地方的GDP，尽可能降低其他地方的GDP。

比如说，各个地方有很强的积极性进行重复建设，而这里微妙之处是，即便重复建设带来过剩产能，但“一损俱损”却可以起到降低其他地方GDP表现的功效。

再比如，处于跨区域河流上游的地方，也将有引入高污染产业的强烈冲动，因为这不但可以提高本地GDP，还可以通过污染排放来降低下游省份的GDP，实有“一举两得”之功。

再比如，在相对缺水的地方，上游的城市或省份也将有过度用水的强烈冲动，因为这不但有助于提高自己的GDP，而且河水断流也可以降低下游的GDP。

由此可见，GDP锦标赛制度乃是一个利弊互见的激励机制。比较公平的评价是，改革开放初期，其正面作用远大于负面作用，但随着时间推移，其负面影响也越来越强。

根据前面对标尺竞争局限性的分析，我们可以从如下几个方面来理解这个问题：

首先，GDP指标的合理性。

改革开放初期，中国是一个典型的“短缺经济”，中国社会的基本矛盾是“人民群众日益增长的物质文化需求与落后的社会生产力之间的矛盾”。“短缺经济”意味着，任何产品都是符合社会需求的，只要生产出来都能够卖掉。所以，这时候GDP基本上可以认为是社会福利的“充分统计量”，因而“以GDP为纲”而让各地方政府进行标尺竞争，就具有很大的合理性。

但是，随着人均收入水平不断提高，人们的需求日益多元化，GDP越来越不能代表整个社会需求。一旦中国社会的主要矛盾转化为“人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾”，那么，适当弱化以GDP锦标赛为特征的标尺竞争就势在必行。

其次，中国各地方禀赋条件差异巨大，而且由于经济集聚效应，这种差异会随着各地区经济发展差距的拉大而拉大。此时，如果继续让各地方进行“标尺竞争”，落后地区将会因为完全没有获胜机会而“破罐子破摔”，而这就失去了标尺竞争的应有之义。

《五分钟经济学》，是复旦大学经济学院寇宗来教授推出的经济学系列作品，旨在用通俗的语言、丰富的案例，阐释经济学的思维逻辑和分析方法。

话题：